Мазмуну:
Video: Үч теңдемелердин системасын жоюу жолу менен кантип чечүүгө болот?
2024 Автор: Miles Stephen | [email protected]. Акыркы өзгөртүү: 2023-12-15 23:38
Башка эки топтомун тандаңыз теңдемелер , айт теңдемелер (2) жана (3) жана жок кылуу ошол эле өзгөрмө. Чечүү the системасы тарабынан түзүлгөн теңдемелер (4) жана (5). Эми z = 3 дегенди алмаштырыңыз теңдеме (4) у табуу. 4-кадамдагы жоопторду колдонуп, каалаганын алмаштырыңыз теңдеме калган өзгөрмө кирет.
Демек, сиз кантип жок кылуу менен теңдеме системасын чечесиз?
Ичинде жоюу ыкмасын сиз кошуу же кемитүү теңдемелер алуу үчүн теңдеме бир өзгөрмөдө. Бир өзгөрмөнүн коэффициенттери карама-каршы болгондо, сиз аны кошосуз теңдемелер өзгөрмөнү жок кылуу үчүн жана бир өзгөрмөнүн коэффициенттери барабар болгондо, сиз аны кемитесиз теңдемелер өзгөрмө жок кылуу.
Андан тышкары, жок кылуу деген эмнени түшүнөсүз? Жоюу ысыраппы, катачылыкпы же атаандаштыкпы, бир нерседен арылуу процесси. Жоюу латын сөзүнөн келип чыккан limen, ал билдирет босого. Римдиктер башына "е" тамгасын кошуп, eliminare этишин түзүшкөн билдирет кууп жиберүү же босогодон ашып эшикти түртүп чыгаруу.
Андан кийин суроо туулат, мен кантип теңдемелер системасын чечем?
Бул кандай болот:
- 1-кадам: өзгөрмөлөрдүн бири үчүн теңдемелердин бирин чечиңиз. y үчүн биринчи теңдемени чечели:
- 2-кадам: Ошол теңдемени башка теңдемеге алмаштырып, х үчүн чечиңиз.
- 3-кадам: Баштапкы теңдемелердин бирине x = 4 x = 4 x=4 алмаштырыңыз жана у үчүн чечиңиз.
Теңдемелер системасын чечүү эмнени билдирет?
А теңдемелер системасы эки же андан көп жыйындысы болуп саналат теңдемелер ошол эле белгисиздердин жыйындысы менен. In чечүү а теңдемелер системасы , биз ар бирин канааттандыра турган белгисиздердин ар бири үчүн баалуулуктарды табууга аракет кылабыз теңдеме ичинде системасы.
Сунушталууда:
Сызыктуу теңдемелер системасын графикалык түрдө кантип чечүүгө болот?
Сызыктуу теңдемелер системасын графикалык түрдө чечүү үчүн бир эле координаттар системасындагы теңдемелердин тең графиктерин түзөбүз. Системанын чечими эки сызык кесилишкен жеринде болот. Эки сызык (-3, -4) менен кесилишет, бул теңдемелердин бул системасынын чечими
Абсолюттук чоңдук теңдемесин алгебралык жол менен кантип чечүүгө болот?
АБСОЛЮТТУК БААЛУУ(ЛАР) БАР ТЕҢДЕМЕЛЕРДИ ЧЕЧҮҮ 1-кадам: Абсолюттук маани туюнтмасын бөлүп алыңыз. 2-кадам: Абсолюттук маанинин ичиндеги санды + жана -га барабар кылып, теңдеменин экинчи тарабындагы чоңдукка коюңуз. 3-кадам: эки теңдемедеги белгисизди чечиңиз. 4-кадам: Жообуңузду аналитикалык же графикалык түрдө текшериңиз
Сызыктуу теңдемелерди графикалык ыкма менен кантип чечүүгө болот?
Графикалык чечимди кол менен (графикалык кагазда) же графиктик калькулятордун жардамы менен жасоого болот. Сызыктуу теңдемелер системасынын графигин түзүү эки түз сызыктын графигиндей эле жөнөкөй. Сызыктын графиги тартылганда, чечим эки сызык кесилишкен жерде (x,y) иреттелген жуп болот (кайчылаш)
Өзгөрмөлөрдү изоляциялоо менен теңдемени кантип чечүүгө болот?
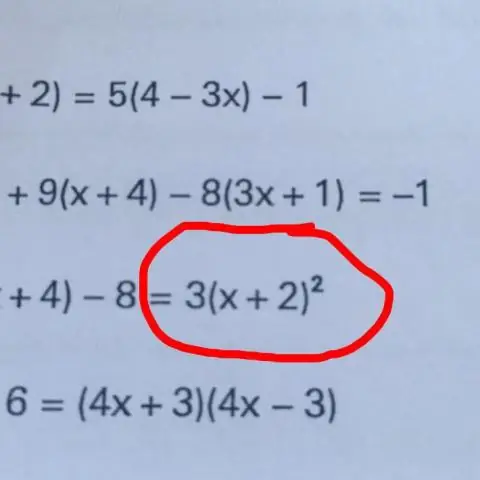
Өзгөрмөлөрдү бөлүп алуунун негизги ыкмасы теңдеменин “эки жагына тең бир нерсе кылуу”, мисалы, теңдеменин эки тарабын бирдей санга кошуу, кемитүү, көбөйтүү же бөлүү. Бул процессти кайталоо менен биз теңдеменин бир тарабында изоляцияланган өзгөрмөнү ала алабыз
Сызыктуу теңдемелер системасын алгебралык жол менен кантип чечүүгө болот?
Эки теңдемедеги жалпы чечимди чечүү үчүн жоюуну колдонуңуз: x + 3y = 4 жана 2x + 5y = 5. x= –5, y= 3. Биринчи теңдемедеги ар бир мүчөнү –2ге көбөйтүңүз (сиз –2x – аласыз) 6y = –8) жана андан кийин эки теңдемедеги мүчөлөрдү кошуңуз. Эми у үчүн –y = –3 чечип, у = 3 болот