Сызыктуу теңдемелер системасын графикалык түрдө кантип чечүүгө болот?

Video: Сызыктуу теңдемелер системасын графикалык түрдө кантип чечүүгө болот?

2024 Автор: Miles Stephen | [email protected]. Акыркы өзгөртүү: 2023-12-15 23:38

үчүн сызыктуу теңдемелер системасын графикалык түрдө чечүү биз график экөө тең теңдемелер ошол эле координатта системасы . The чечим га системасы эки сызык кесилишкен жерде болот. Эки сызык (-3, -4) менен кесилишет чечим буга системасы нын теңдемелер.

Ушундай жол менен сызыктуу теңдемелер системасын график аркылуу кантип чечүүгө болот?

үчүн чечүү а сызыктуу теңдемелердин системасы график боюнча , адегенде эки бар экенин текшериңиз сызыктуу теңдемелер . Анда, график ар бири менен көрсөтүлгөн сызык теңдеме жана эки сызык бири-бири менен кесилишкен жерди көрүңүз. Кесилиш чекитинин х жана у координаталары чечимдин чечими болот системасы нын теңдемелер !

Андан кийин суроо туулат, сызыктуу теңдемени чечүү үчүн кандай кадамдар бар?

1-кадам: Зарыл болсо, ар бир тарапты жөнөкөйлөтүү.
2-кадам: Add./Sub колдонуңуз. Өзгөрмө терминди бир тарапка, бардык башка терминдерди экинчи тарапка жылдыруу үчүн касиеттер.
3-кадам: Mult./Div.
4-кадам: Жообуңузду текшериңиз.
Мен бул сызыктуу теңдемелерге жакындоонун эң тез жана эң оңой жолу деп эсептейм.
Мисал 6: Өзгөрмө үчүн чечиңиз.

Мындан тышкары, сызыктуу системаны текшерүү жана чечүү үчүн графикти кантип колдоносуз?

колдонуу үчүн график жана текшерүү ыкмасы чечүү а системасы нын сызыктуу эки өзгөрмөлүү теңдемелер үчүн төмөнкү кадамдарды колдонуңуз. Ар бир теңдемени оңой болгон формада жазыңыз график . График эки теңдеме бир координаталык тегиздикте. кесилишкен чекиттин координаталарын эсептегиле.

Графигин көрсөтпөстөн теңдемелер системасын кантип чечүүгө болот?

үчүн системаны чечүү сызыктуу графиксиз теңдеме , алмаштыруу ыкмасын колдоно аласыз. Бул ыкма иштейт чечүү линиялыктардын бири теңдемелер өзгөрмөлөрдүн бири үчүн, андан кийин башка сызыктуу бир эле өзгөрмө үчүн бул маанини алмаштыруу теңдеме жана чечүү башка өзгөрмө үчүн.

Сунушталууда:

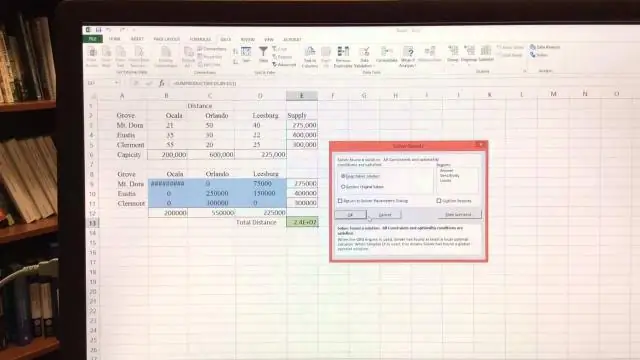
Excelде LPди графикалык түрдө кантип чечесиз?

ВИДЕО Ушундай жол менен, маселени графикалык түрдө кантип чечесиз? үчүн чечүү теңдеме билдирүүнү туура кылган бардык баалуулуктарды табуу дегенди билдирет. үчүн чечүү теңдеме графикалык түрдө , теңдеменин ар бир тарабы, мүчөсү үчүн графигин тартыңыз жана ийри сызыктар кай жерде кесилишкенин көрүңүз.

Сызыктуу теңдемелерди графикалык ыкма менен кантип чечүүгө болот?

Графикалык чечимди кол менен (графикалык кагазда) же графиктик калькулятордун жардамы менен жасоого болот. Сызыктуу теңдемелер системасынын графигин түзүү эки түз сызыктын графигиндей эле жөнөкөй. Сызыктын графиги тартылганда, чечим эки сызык кесилишкен жерде (x,y) иреттелген жуп болот (кайчылаш)

Үч теңдемелердин системасын жоюу жолу менен кантип чечүүгө болот?

Эки теңдеменин башка топтомун тандаңыз, (2) жана (3) теңдемелерин айтыңыз жана бир эле өзгөрмөнү жок кылыңыз. (4) жана (5) теңдемелери боюнча түзүлгөн системаны чечиңиз. Эми, у табуу үчүн (4) теңдемеге z = 3 коюңуз. 4-кадамдагы жоопторду колдонуңуз жана калган өзгөрмө катышкан каалаган теңдемеге алмаштырыңыз

Сызыктуу теңдемелер системасын алгебралык жол менен кантип чечүүгө болот?

Эки теңдемедеги жалпы чечимди чечүү үчүн жоюуну колдонуңуз: x + 3y = 4 жана 2x + 5y = 5. x= –5, y= 3. Биринчи теңдемедеги ар бир мүчөнү –2ге көбөйтүңүз (сиз –2x – аласыз) 6y = –8) жана андан кийин эки теңдемедеги мүчөлөрдү кошуңуз. Эми у үчүн –y = –3 чечип, у = 3 болот