
- Автор Miles Stephen [email protected].
- Public 2023-12-15 23:38.
- Акыркы өзгөртүү 2025-01-22 17:03.
Математика боюнча, а тескери функция (же каршы функция ) болуп саналат функция бул башканы "кайтарат" функция : Эгерде функция x киргизүүгө колдонулган f y натыйжасын берет, андан кийин аны колдонот тескери функция g менен y натыйжасы x берет, жана тескерисинче, б.а., f(x) = y, эгерде жана эгерде g(y) = x болсо гана.
Демек, эсептөөдө функциянын тескерисин кантип табасыз?
Функциянын тескерисин табуу
- Биринчиден, f(x) ды у менен алмаштырыңыз.
- Ар бир хды у менен алмаштырыңыз жана ар бир уду х менен алмаштырыңыз.
- y үчүн 2-кадамдагы теңдемени чечиңиз.
- y ордуна f−1(x) f − 1 (x).
- (f∘f−1)(x)=x (f ∘ f − 1) (x) = x жана (f−1∘f)(x)=x (f − 1 ∘ f) экенин текшерүү менен ишиңизди текшериңиз. (x) = x экөө тең чындык.
тескери функциянын мисалы деген эмне? Тескери функциялар , эң жалпы мааниде, болуп саналат функциялары бул бири-бирин "тескери". үчүн мисал , эгерде f адан бга чейин кабыл алса, анда тескери , f − 1 f^{-1} f−1f, башталыш үстү, минус, 1, аягы, bдан ага чейин болушу керек.
Бул жерде тескери функцияларды кантип айырмалайсыз?
Тескери тригонометриялык функциялардын туундулары
- g(x)=sin−1x туундусун табуу үчүн тескери функция теоремасын колдонуңуз.
- [−π2, π2] аралыктагы х үчүн f(x)=sinx g(x)=sin−1x тескериси болгондуктан, f′(x) табуу менен баштаңыз.
- f′(x)=cosx.
- f′(g(x))=cos(sin−1x)=√1−x2.
- g′(x)=ddx(sin−1x)=1f′(g(x))=1√1−x2.
Өзүнө тескери функция деген эмне?
А өзүнө тескери функция болуп саналат функция f, y=f(x), өзгөчө касиети менен ff(x)=x, же башка жол менен жазылган, f(x)=f−1(x)
Сунушталууда:
Көрсөткүчтүү функцияга тескери функция деген эмне?
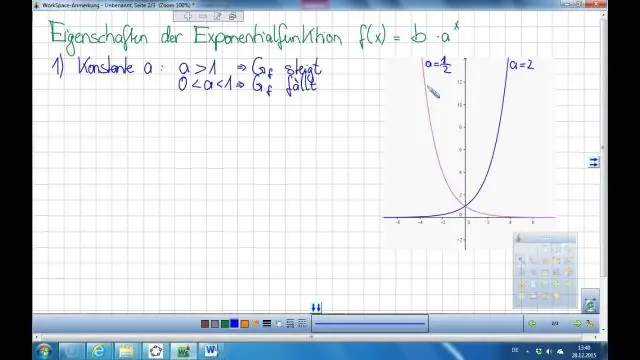
Y = ax экспоненциалдык функциянын тескериси х = ай. Логарифмдик функция у = логакс экспоненциалдык теңдемеге эквиваленттүү деп аныкталат x = ay
Эсептөөдөгү үзгүлтүксүз функция деген эмне?
Эгерде функция интервалдагы ар бир мааниде үзгүлтүксүз болсо, анда функция ошол интервалда үзгүлтүксүз деп айтабыз. Ал эми кандайдыр бир интервалда функция үзгүлтүксүз болсо, анда биз аны жөн гана үзгүлтүксүз функция дейбиз. Эсептөө негизинен өз чөйрөлөрүндөгү ар бир мааниде үзгүлтүксүз болгон функциялар жөнүндө
Эсептөөдөгү курама функция деген эмне?

Ушул сыяктуу эки (же андан көп) функцияны бириктирүү функцияларды түзүү, ал эми пайда болгон функция курама функция деп аталат. Композиттик функция эрежеси бизге тезирээк жолду көрсөтөт. 7-эреже (Композиттик функция эрежеси (чынжыр эрежеси катары да белгилүү)) Эгерде f(x) = h(g(x)) анда f (x) = h (g(x)) × g (x)
Эсептөөдөгү үзгүлтүксүздүк деген эмне?

Үзгүлтүксүздүк деген эмне? Эсептөөдө функция x = a учурунда үзгүлтүксүз болот, эгерде - жана эгерде - төмөндөгү үч шарт тең аткарылса: Функция x = a учурунда аныкталган; башкача айтканда, f(a) реалдуу санга барабар. x а жакындаган сайын функциянын чеги бар
Эсептөөдөгү абсолюттук маани деген эмне?

Абсолюттук маани функциясы | | менен аныкталат. х абсолюттук мааниси х жана 0 ортосундагы аралыкты берет. Ал ар дайым оң же нөл болот. Мисалы, |3| = 3, |-3| = 3, |0|=0
