Мазмуну:
Video: Сызыктуу функциялардын чыныгы турмуштук мисалдары кандай?
2024 Автор: Miles Stephen | [email protected]. Акыркы өзгөртүү: 2023-12-15 23:38
Жооп: Кимдир бирөө мага бере алабы мисал нын сызыктуу функциялар реалдуу жашоо кырдаал? Сызыктуу функциялар каалаган убакта болот а туруктуу өзгөрүү ылдамдыгы.
Чыныгы турмуштук мисалдар:
- 1, 2, 3-күндө керектелген ток табылууда…
- Сен ал а ижарага машина.
- Сиз айдап барасыз а унаа дар the ылдамдыгы 60 км/саат.
Муну эске алганда, сызыктуу функциянын чыныгы турмуштук мисалы кандай?
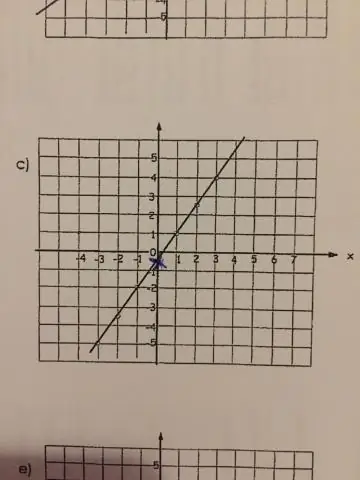
Мисал : Ылдамдыкты сүрөттөөчү сызыктын графигин тартыңыз. Эңкейүү саатына 5 миль болгон жана башталгыч чекит (0, 0) болгондон кийин, y -кесилиши 0. Ошентип биздин финал функция y=5x y = 5 x болот. Аралык жана убакыт графиги: y=5x y = 5 x графиги. Эки өзгөрмө убакыт (x) жана аралык (y) болуп саналат.
Кошумча, сызыктуу теңдеменин мисалы кандай? Мисал : y = 2x + 1 - а сызыктуу теңдеме : y = 2x+1 графиги түз сызык. x көбөйгөндө, у эки эсе тез өсөт, ошондуктан бизге 2x керек. x 0 болгондо, у мурунтан эле 1.
Ошо сыяктуу эле, адамдар чыныгы жашоодо функцияларды кайда колдонобуз?
Бул жерде бир нече мисал келтирилген:
- Circle of a Circle - Айлананын айланасы анын диаметринин функциясы болуп саналат.
- Көлөкө - полдун боюндагы адамдын көлөкөсүнүн узундугу анын боюнун функциясы болуп саналат.
- Унаа айдоо - Унаа айдап жатканда сиздин жайгашкан жериңиз убакыттын функциясы болуп саналат.
Чыныгы жашоодо сызыктуу теңсиздиктер кантип колдонулат?
системасы сызыктуу теңсиздиктер тез-тез колдонулган маселенин эң жакшы жолун аныктоо. Бул чечим кирешени көбөйтүү үчүн канча продуктуну өндүрүү керек экендигин аныктоо сыяктуу жөнөкөй же пациентке берүү үчүн дарылардын туура айкалышын аныктоо сыяктуу татаал болушу мүмкүн.
Сунушталууда:
Функциялардын параметрлеринин үй-бүлөлөрү жана графиктердин сыпаттамалары кандай байланышта?
Функциялардын үй-бүлөлөрү - бул форманын эң негизги мисалы болгон ата-эне функциясы менен таанышканыңызда аларды графикке түшүрүүнү жеңилдеткен окшоштуктары бар функциялардын топтору. Параметр белгилүү бир теңдемени түзүү үчүн белгилүү бир маанини алган жалпы теңдемедеги өзгөрмө
Сызыктуу теңсиздиктер менен сызыктуу теңдемелерди чечүү кандайча окшош?
Сызыктуу теңдемелерди чечүү сызыктуу теңдемелерди чыгарууга абдан окшош. Негизги айырмачылык - терс санга бөлүүдө же көбөйтүүдө теңсиздик белгисин которот. Сызыктуу теңсиздиктердин графиктерин түзүү дагы бир нече айырмачылыктарга ээ. Көлөкөлүү бөлүгү сызыктуу теңсиздик чын болгон маанилерди камтыйт
Теңдеме сызыктуу же сызыктуу эмес экенин кантип билесиз?
Теңдемени колдонуу Теңдемени мүмкүн болушунча у = mx + b түрүнө жөнөкөйлөтүңүз. Теңдемеңиздин көрсөткүчтөрү бар-жогун текшериңиз. Эгерде анын көрсөткүчтөрү бар болсо, анда ал сызыктуу эмес. Эгер теңдемеңиздин көрсөткүчтөрү жок болсо, анда ал сызыктуу болот
Бардык сызыктуу функциялардын тескери функциялары барбы?
Туруктуу эмес сызыктуу функцияларга тескери. Сызыктуу функция туруктуу эмес, же башкача айтканда нөл эмес эңкейишке ээ болсо, инверсивдүү болот. Сиз y = x диагоналынын үстүнөн баштапкы сызыкты чагылдыруу менен тескерисин алгебралык же графикалык түрдө таба аласыз
Сызыктуу функциялардын максаты эмне?
Сызыктуу функция түз сызыктын графигин түзүүчү каалаган функция. Бул математикалык жактан эмнени билдирет, функциянын көрсөткүчтөрү же күчү жок бир же эки өзгөрмө бар. Эгерде функцияда көбүрөөк өзгөрмөлөр болсо, функция сызыктуу функция бойдон калышы үчүн өзгөрмөлөр туруктуу же белгилүү өзгөрмө болушу керек