
Мазмуну:
- Автор Miles Stephen [email protected].
- Public 2023-12-15 23:38.
- Акыркы өзгөртүү 2025-01-22 17:04.
табыңыз аймак ичинде кардиоид r = 1 + cos θ. Жооп бер кардиоид жүрөк формасында болгондуктан ушундай аталып калган. Радиалдык тилкелерди колдонуу менен интеграциянын чеги (ички) r 0дөн 1ге чейин + cos θ; (тышкы) θ 0дөн 2πге чейин. Ошентип, аймак болуп саналат. 2π 1+cos θ dA = r dr dθ.
Мындан тышкары, полярдык аймактын аянтын кантип табасыз?
r=f(θ) α≦θ≦β теңдемеси менен аныкталган полярдык координаттардагы аймактын аянты A=1 интегралы менен берилген. 2 ∫βα[f(θ)] 2 dθ. ортосундагы аймакты табуу үчүн эки полярдык координаталар системасындагы ийри сызыктар үчүн, адегенде кесилишкен чекиттерди таап, андан кийин тиешелүү аймактарды алып салыңыз.
Ошондой эле, сиз Cos 2xти кантип бириктиресиз? The интегралдык нын cos ( 2x ) (1/2)син( 2x ) + C, мында С - туруктуу.
Бул жерде ийри сызыктын астындагы аянттын формуласы кандай?
The ийри сызык астындагы аймак эки чекиттин ортосундагы эки чекиттин ортосунда аныкталган интегралды жасоо менен аныкталат. табуу үчүн астындагы аймак the ийри y = f(x) x = a & x = b ортосунда, y = f(x) а менен b чектеринин ортосунда интегралдагыла. Бул аймак берилген чектер менен интеграцияны колдонуу менен эсептелиши мүмкүн.
Параметрдик теңдемелерди кантип чечесиз?
1-мисал:
- y=x2+5 теңдемеси үчүн параметрлик теңдемелердин жыйындысын табыңыз.
- t ге барабар өзгөрмөнүн каалаган бирине дайындаңыз. (x = t деп айтабыз).
- Анда берилген теңдемени y=t2+5 катары кайра жазууга болот.
- Демек, параметрдик теңдемелердин жыйындысы x = t жана y=t2+5.
Сунушталууда:
Кубдун бетинин аянты менен көлөмүнүн ортосунда кандай байланыш бар?

Мындан кичине кубиктердин бетинин аянты чоңураак кубиктерге караганда көлөмгө салыштырмалуу чоңураак (бул жерде көлөм беттин аянтына салыштырмалуу чоң). объекттин көлөмү чоңойгон сайын (формасын өзгөртпөстөн) бул катыш төмөндөй турганын ачык көрсөтүп турат
Жер бетинин аянты кулаганга кандай таасир этет?

Аба каршылыгы аракет кылганда, кулаганда ылдамдануу g дан аз болот, анткени абанын каршылыгы кулаган нерселердин кыймылына аны жайлатып таасир этет. Абанын каршылыгы эки маанилүү фактордон көз каранды - объекттин ылдамдыгы жана анын бетинин аянты. Объекттин бетинин аянтын көбөйтүү анын ылдамдыгын азайтат
Бетинин аянты менен каптал аянтынын ортосунда кандай айырма бар?
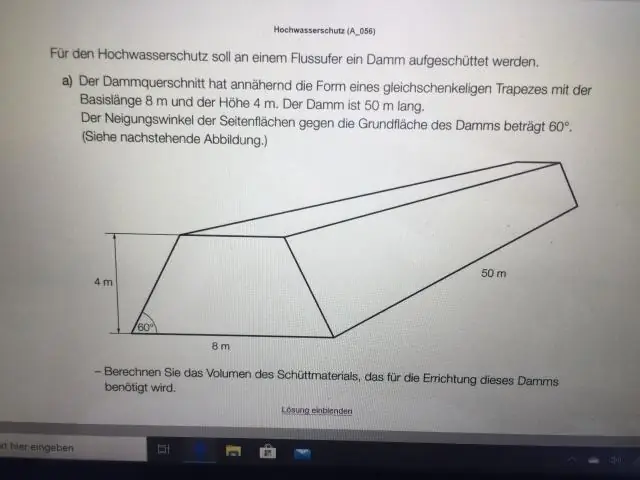
Каптал бетинин аянты - базанын аянтын кошпогондо, бардык тараптардын аянты. Катуу нерсенин жалпы бетинин аянты – бул катуу нерсенин бардык беттеринин аянттарынын суммасы
Шардын бетинин аянты менен көлөмүнүн ортосунда кандай байланыш бар?

Сфера үчүн беттин аянты S= 4*Pi*R*R, мында R – шардын радиусу жана Pi – 3,1415 Сферанын көлөмү V= 4*Pi*R*R*R/3. Ошентип, шар үчүн беттин аянтынын көлөмгө болгон катышы төмөнкүчө берилет: S/V = 3/R
Фигуранын бетинин аянты кандай?

Беттин аянты - 3D формасындагы бардык беттердин (же беттердин) аянттарынын суммасы. Кубоиддин 6 тик бурчтуу бети бар. Кубоиддин бетинин аянтын табуу үчүн бардык 6 беттин аянттарын кошуу керек. Ошондой эле призманын узундугун (l), туурасын (w) жана бийиктигин (h) белгилей алабыз жана беттин аянтын табуу үчүн SA=2lw+2lh+2hw формуласын колдонсок болот
