Video: Бөлүм эрежесинин ордуна продукт эрежесин колдоно аласызбы?
2024 Автор: Miles Stephen | [email protected]. Акыркы өзгөртүү: 2023-12-15 23:38
Мунун эки себеби бар бөлүү эрежеси болот бийликтен жогору болуу эреже плюс продукт эрежеси айырмалоодо а бөлүк : Ал жыйынтыкты жөнөкөйлөтүүдө жалпы бөлүүчүлөрдү сактайт. Эгерде колдоносуз күч эреже плюс продукт эрежеси , сен натыйжаны жөнөкөйлөтүү үчүн көп учурда жалпы бөлүүчү табуу керек.
Ошо сыяктуу эле, кимдир бирөө суроо бериши мүмкүн, продукт эрежеси менен бөлүү эрежесинин ортосунда кандай айырма бар?
The Продукт эрежеси а-нын туундусу экенин айтат продукт эки функциянын биринчи функциясынын экинчи функциянын туундусунун жана экинчи функциянын биринчи функциянын туундусунун эсеси. The Продукт эрежеси туунду болгондо колдонулушу керек бөлүк эки функцияны аткаруу керек.
Ошондой эле билесизби, продукт эрежеси кантип иштейт? The продукт эрежеси Эсептөөдө сизден бир нече же бир нече кичине функцияларды көбөйтүү болгон функциянын туундусун алуу суралганда колдонулат. Башкача айтканда, f(x) функциясы а продукт функциялардын, эгерде ал болот g(x)h(x) жана башкалар катары жазылат. Бул функция а продукт эки кичинекей функция.
Ушундай жол менен, эмне үчүн биз бөлүү эрежесин колдонобуз?
менен киришүү Бөлүштүрүүчү эреже The бөлүү эрежеси туундуларды эсептөөнүн негизги эрежелеринин акыркысы болуп саналат жана ал биринчи кезекте, эгерде сен башка функцияга бөлүнгөн функцияга ээ жана сен келет алуу ошонун туундусу.
Бөлүштүрүүчү эреженин формуласы кандай?
The бөлүү эрежеси болуп саналат формула а-нын туундусун алуу үчүн бөлүк эки функциянын. The формула f(x) дын g(x) га бөлүнгөн туундусун табуу үчүн төмөнкүлөр керек деп айтылат: f(x) туундусунун g(x) эсесин алуу. Анда ошол көбөйтүндүн ичинен f(x) көбөйтүлгөнүн g(x) туундусун алып салуу керек.
Сунушталууда:
Продукт жана бөлүү эрежесин кантип колдоносуз?
Продукт эрежеси эки функциянын продуктунун туундусу биринчи функциянын экинчи функциянын туундусуна жана экинчи функциянын биринчи функциянын туундусуна кошулганын айтат. Продукт эрежеси эки функциянын бөлүктөрүнүн туундусун алуу үчүн колдонулушу керек
Продукт же бөлүктүн эрежесин качан колдонуу керектигин кайдан билесиз?
Функциялардын бөлүнүшү. Ошентип, эки функциянын көбөйүшүн көргөн сайын продукт эрежесин жана бөлүү учурунда бөлүү эрежесин колдонуңуз. Функцияда көбөйтүү да, бөлүү да бар болсо, эки эрежени тең тиешелүү түрдө колдонуңуз. Эгер сиз жалпы теңдемени көрсөңүз, бул, сыяктуу бир нерсе, бул жерде жалгыз жагынан функция
Продукт эрежеси менен чынжыр эрежесинин ортосунда кандай айырма бар?
Жалпысынан f(g(x)) сыяктуу "функциянын функциясын" дифференциялоодо чынжыр эрежесин колдонобуз. Жалпысынан f(x)g(x) сыяктуу чогуу көбөйтүлгөн эки функцияны дифференциялоодо продукт эрежесин колдонобуз. Бирок алар өзүнчө функциялар экенин эске алыңыз: бири экинчисине жооп бербейт
Кайчылаш продукт үчүн оң кол эрежесин кантип колдоносуз?
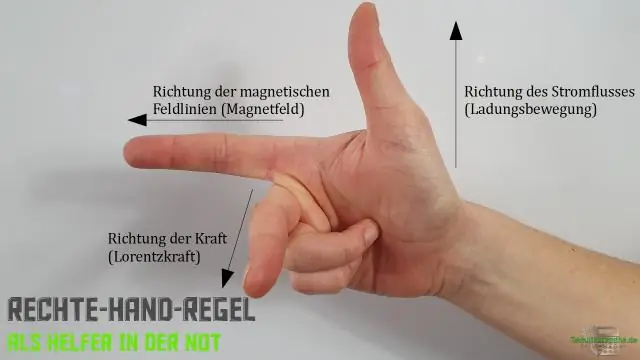
Оң кол эрежеси векторлордун кайчылаш көбөйтүндүсүнүн теориясы оң колду жайлоо жана куйруктан куйрукка, оң колду тегиздөө, аны көздөй сунуу жана андан кийин манжаларды бурч жасаган багытта тармалдоо менен аныкталат деп айтылат. Баш бармак андан кийин багытты көрсөтөт
Бөлүм эрежесин продукт эрежесине кантип айландырасыз?
Бөлүм эрежеси продукт жана чынжыр эрежелерин колдонуу катары каралышы мүмкүн. Эгерде Q(x) = f(x)/g(x), анда Q(x) = f(x) * 1/(g(x)). Q(x) айырмалоо үчүн продукт эрежесин колдоно аласыз, ал эми 1/(g(x)) чынжыр эрежеси аркылуу u = g(x) жана 1/(g(x)) = 1/u менен дифференцияланса болот