Video: Трансформация бирден экенин кантип билесиз?
2024 Автор: Miles Stephen | [email protected]. Акыркы өзгөртүү: 2023-12-15 23:38
Качан сызыктуу трансформация матрицанын терминдеринде сүрөттөлөт, ал оңой экендигин аныктоо сызыктуу трансформация бирден болуп саналат же матрицанын мамычаларынын сызыктуу көз карандылыгын текшерүү менен эмес. Эгерде мамычалар сызыктуу көз карандысыз, сызыктуу трансформация бирден болуп саналат.
Бул жагынан алганда, сызыктуу трансформация бирден болсо, бул эмнени билдирет?
Бирден-бир сызыктуу трансформациялар . Аныктама : А сызыктуу трансформация айырмаланган чекиттерди/векторлорду бири-биринен айырмаланган чекиттерге/векторлорго картага түшүрүү а деп айтылат бирден-бир трансформация же инъекция трансформация . Ошентип, ар бир вектор үчүн так бар бир вектор ушундай.
Ошондой эле суроо берилиши мүмкүн, сызыктуу трансформация бирден эмес, бирден болушу мүмкүнбү? Матрицалык терминдер менен айтканда, бул а трансформация А матрицасы менен үстүнө эгерде Ax=b диапазондогу каалаган b үчүн чечимге ээ болсо. Эгер трансформация болуп саналат үстүнө, бирок бирден эмес , сен болот Доменди диапазонго туура келүү үчүн өтө көп векторлор бар деп ойло.
Бул жерде матрица бирден эмес, бирден болушу мүмкүнбү?
Атап айтканда, жалгыз матрицалар ошол болот экөө тең болсун бирге бир жана үстүнө төрт бурчтуу матрицалар . Башка жагынан алганда, сен болот бар а m×n матрица м<н менен башкача айтканда үстүнө , же бир ушул үстүнө эмес . Жана сен болот m×n бар матрицалар м> н менен бирге бир , жана матрицалар ошол бирден эмес.
Сызыктуу трансформацияны кантип далилдейсиз?
Ар бир y ∈ Y үчүн f(x) = y болгон жок дегенде бир x ∈ X бар. f кодоменинин ар бир элементи кандайдыр бир киргизүү үчүн чыгаруу болуп саналат. А экендигин аныктай алабыз сызыктуу трансформация бирден же үстүнө анын стандарттык матрицасынын мамычаларын текшерүү (жана саптарды азайтуу).
Сунушталууда:
Бир нерсенин функция экенин же жокпу, кантип билесиз?
ЖООП: Жооптун үлгүсү: Домендин ар бир элементи диапазонун так бир элементи менен жупташканын аныктай аласыз. Мисалы, эгер график берилсе, сиз вертикалдык сызык тестин колдонсоңуз болот; эгерде вертикалдык сызык графты бир нече жолу кессе, анда график көрсөткөн байланыш функция эмес
Теңдеменин функция экенин же жок экенин кантип билесиз?
Y үчүн чечүү жолу менен теңдеменин функция экендигин аныктоо салыштырмалуу оңой. Сизге теңдеме жана x үчүн белгилүү бир маани берилгенде, ал х-мааниси үчүн бир гана тиешелүү у-маани болушу керек. Бирок, y2 = x + 5 функция эмес; эгерде сиз x = 4 деп ойлосоңуз, анда y2 = 4 болот. + 5= 9
Кошулма молекулалык экенин кантип билесиз?
Аралаш иондук/молекулярдык кошулмаларды атоо. Кошулмаларды атоодо, биринчиден, бул кошулма иондук же молекулалык экенин аныктоо керек. Курамдагы элементтерди карагыла. *Иондук бирикмелер металлдарды да, металл эместерди да, же жок дегенде бир көп атомдуу ионду камтыйт. *Молекулярдык бирикмелерде металл эместер гана болот
Фазалык жылыш оң же терс экенин кантип билесиз?
Эгерде фазалык жылыш нөлгө барабар болсо, ийри сызык башатынан башталат, бирок фазалык жылышка жараша солго же оңго жылышы мүмкүн. Терс фазалык жылыш оңго кыймылды, ал эми оң фазалык жылыш солго кыймылды көрсөтөт
Эвери жана анын тобу трансформация үчүн кайсы молекула эң маанилүү экенин кантип аныкташкан?
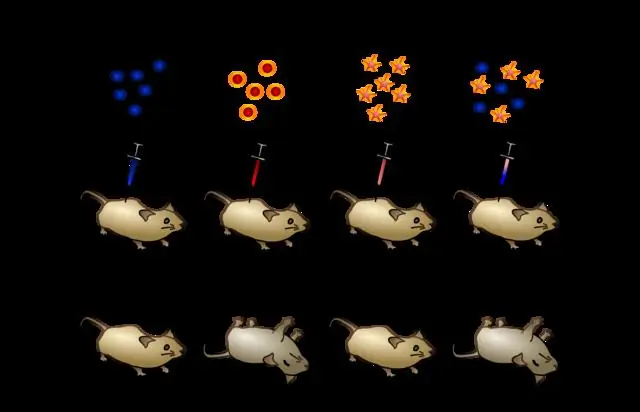
Эвери жана анын тобу трансформация үчүн кайсы молекула эң маанилүү экенин кантип аныкташканын кыскача сүрөттөп бериңиз. Эвери жана анын тобу ысыкта өлтүрүлгөн бактериялардын экстрактысында эки башка ферментти колдонушкан. Бири ДНКны жок кылса, экинчиси баарын жок кылган. Алар ДНК бар кезде трансформация дагы эле болгонун аныкташкан