
Мазмуну:
- Автор Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:38.
- Акыркы өзгөртүү 2025-01-22 17:03.
Сүрөттөө а кеңейтүү масштаб факторун (же катышын) жана борборун камтыйт кеңейтүү . борбору кеңейтүү тегиздиктеги туруктуу чекит болуп саналат. Эгерде масштаб коэффициенти 1ден чоң, сүрөт чоңойтулган (чоюу). Эгерде масштаб коэффициенти 0 жана 1 ортосунда, сүрөт кичирейтүү (кичирейүү).
Ушуга байланыштуу кеңейүү масштабынын фактору деген эмне?
А кеңейтүү сүрөттүн өлчөмүн өзгөрткөн трансформациянын бир түрү. The масштаб фактору , кээде скаляр деп аталат фактор , сүрөттөлүштүн канчалык чоң же кичине экенин өлчөйт. Төмөндө ар бир түрүнүн сүрөтү кеңейтүү (бирөөсү чоңоюп, бири кичирейет).
Ошондой эле суроо бериши мүмкүн, сиз сүрөттү кантип кеңейтесиз? Координаталык тегиздиктеги көпчүлүк кеңейүүлөр баштын борбору катары (0, 0) башын колдонот кеңейтүү . ΔABC менен баштап, тартыңыз кеңейтүү сүрөтү борбору башатында жана масштабдык фактору эки болгон үч бурчтуктун. Баштапкы үч бурчтуктун ар бир координаты масштаб коэффициентине (x2) көбөйтүлгөнүнө көңүл буруңуз.
Анын вертикалдуу кеңейүүсүн кантип табасыз?
Вертикалдуу кеңейүү
- y = C * f(x) Жана ошондой эле биз баштапкы теңдемедеги у-ну y/C катары алмаштыра алабыз.
- 1-мисал: y = x функциясы үчүн вертикалдык кеңейүүнү жасаңыз2 шкала коэффициенти менен 3.
- Чечим: у = х2
- 2-мисал: у = 4х2 графигин алуу үчүн у = x2 графигиндеги кеңейүүнү тандаңыз.
- чечим:
- 1-мисал:
- Чечим:
- График.
Масштаб коэффициентин кантип табасыз?
табуу үчүн а масштаб фактору эки окшош фигуранын ортосунда, эки тиешелүү тарапты таап, эки тараптын катышын жаз. Эгер сиз кичинекей фигура менен баштасаңыз, анда сиздин масштабдык фактор бирден аз болот. Эгер сиз чоңураак фигура менен баштасаңыз, анда сиздин масштаб фактору бирден чоң болот.
Сунушталууда:
Теңдеменин функция экенин же жок экенин кантип билесиз?

Y үчүн чечүү жолу менен теңдеменин функция экендигин аныктоо салыштырмалуу оңой. Сизге теңдеме жана x үчүн белгилүү бир маани берилгенде, ал х-мааниси үчүн бир гана тиешелүү у-маани болушу керек. Бирок, y2 = x + 5 функция эмес; эгерде сиз x = 4 деп ойлосоңуз, анда y2 = 4 болот. + 5= 9
Трансформациянын эффективдүүлүгүнүн формуласы кандай?
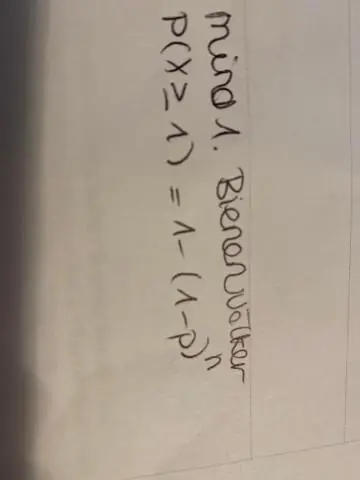
Аны ийгиликтүү трансформациялоо процессинде колдонулган ДНКнын санына бөлүү жолу менен эсептөөгө болот
Реакцияда оң дельта S бар экенин кантип билүүгө болот?

Физикалык же химиялык реакциянын энтропиянын көбөйүшү же азайышы болорун болжолдоп жатканда, учурдагы түрлөрдүн фазаларын караңыз. Айтууга жардам берүү үчүн "Акылдуу кичинекей текелерди" эстеңиз. Биз "эгер энтропия көбөйсө, Delta S оң" жана "энтропия азайса, Delta S терс" деп айтабыз
Элементтин металлоид экенин кантип билсе болот?

Металоид – металлдар менен металл эместердин ортосундагы аралык касиеттерге ээ болгон элемент. Металлоиддерди жарым металлдар деп да атоого болот. Мезгилдик таблицада көбүнчө тепкич сызыгын чектеп турган сары түстөгү элементтер металлоиддер болуп эсептелет
Эки теңдеменин параллелдүү экенин кантип билсе болот?

Алардын теңдемелеринен эки сызык параллель экендигин алардын жантаймаларын салыштырып аныктай алабыз. Эгерде эңкейиштер бирдей жана у-кесилиштери ар башка болсо, сызыктар параллелдүү. Эңкейиштер башка болсо, сызыктар параллелдүү эмес. Параллель сызыктардан айырмаланып, перпендикуляр сызыктар кесилишет
