Мазмуну:
Video: Теңдеменин графигин этап-этабы менен кантип түзөсүз?
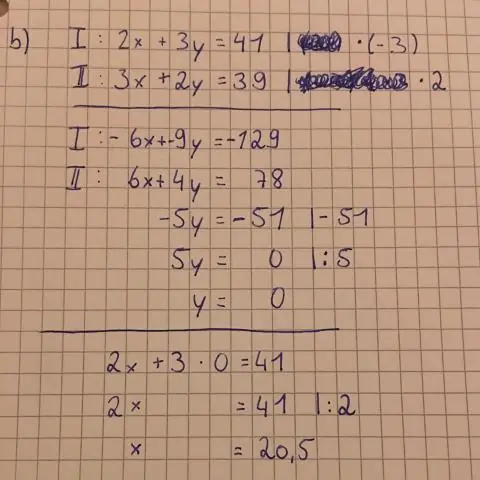
2024 Автор: Miles Stephen | [email protected]. Акыркы өзгөртүү: 2023-12-15 23:38
Бул жерде кээ бир кадамдарды аткаруу керек:
- x = 0 коюңуз теңдеме жана у үчүн чечиңиз.
- (0, y) чекиттин у огунун графигин түзүңүз.
- y = 0 коюңуз теңдеме жана x үчүн чечүү.
- (x, 0) чекиттин х огунун графигин түзүңүз.
- Эки чекиттин ортосуна түз сызык тарткыла.
Ошо сыяктуу эле, сиз графиктик теңдемени этап-этабы менен кантип чечесиз?
Кадамдар
- Сызыктуу теңдеме y = mx + b түрүндө экенин текшериңиз.
- Y огуна b санын сызыңыз.
- mди бөлчөккө айландыруу.
- Эңкейүүнү колдонуп сызыкты bдан узарта баштаңыз же чуркоодон өйдө көтөрүлүңүз.
- Сызыкты узартууну улантыңыз, сызгычты колдонуп, эңкейишти, м, жол көрсөтүүчү катары колдонуңуз.
Ошондой эле, сиз теңдемеден сызыкты кантип графикке саласыз? Сызыктуу теңдеменин графигин түзүү үчүн биз эңкейишти жана у кесилишин колдонсок болот.
- Графиктен у кесилишинин ордун табыңыз жана чекитти түзүңүз.
- Ушул жерден экинчи чекитти таап, аны пландоо үчүн эңкейишти колдонуңуз.
- Эки чекитти бириктирген сызыкты тарткыла.
Графиктен теңдемени кантип түзүүгө болот?
үчүн жаз а теңдеме эңкейиш-кесилген формада, берилген а график ошонун теңдеме , сызыктан эки чекит тандап, эңкейишти табуу үчүн аларды колдонуңуз. Бул м-нин мааниси теңдеме . Андан кийин, у-кесилишинин координаталарын табыңыз - бул (0, b) формасында болушу керек. y- координатасы б-нын мааниси теңдеме.
Теңдемелер системасын кантип табасыз?
Бул кандай болот:
- 1-кадам: өзгөрмөлөрдүн бири үчүн теңдемелердин бирин чечиңиз.
- 2-кадам: Ошол теңдемени башка теңдемеге алмаштырып, х үчүн чечиңиз.
- 3-кадам: Баштапкы теңдемелердин бирине x = 4 x = 4 x=4 алмаштырыңыз жана у үчүн чечиңиз.
Сунушталууда:
Гиперболалык функциянын графигин кантип түзөсүз?
Гиперболалык функциялардын графиктери sinh(x) = (e x - e -x)/2. cosh(x) = (e x + e -x)/2. tanh(x) = sinh(x) / cosh(x) = (ex - e -x) / (ex + e -x) coth(x) = cosh(x) / sinh(x) = (ex + e - x) / (ex - e -x) sech(x) = 1 / cosh(x) = 2 / (ex + e -x) csch(x) = 1 / sinh(x) = 2 / (ex - e - x)
Ылдамдыктын жана ылдамдануунун графигин кантип түзөсүз?
Принцип ылдамдык-убакыт графигиндеги сызыктын жантайышы объекттин ылдамдануусу жөнүндө пайдалуу маалыматты ачып берет. ылдамдануу нөл болсо, анда жантаюу нөл (б.а., горизонталдуу сызык). Эгерде ылдамдануу оң болсо, анда жантаюу оң болот (б.а., өйдө карай жантайыңкы сызык)
Ата-энелик функциянын графигин кантип түзөсүз?
Y=x2 же f(x) = x2 функциясы квадраттык функция болуп саналат жана бардык башка квадраттык функциялар үчүн негизги график болуп саналат. f(x) = x2 функциясынын графигин түзүүнүн жарлыгы (0, 0) (башкы) чекитинен башталып, чокусу деп аталган чекитти белгилөө. (0, 0) чекит ата-энелик функциянын чокусу гана экенин эске алыңыз
Биологиянын графигин кантип түзөсүз?
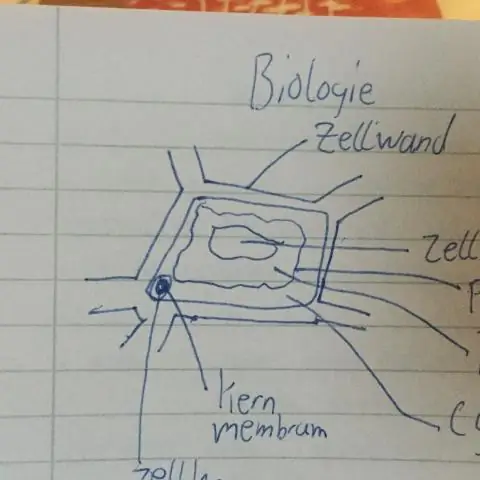
График кантип түзүлөт Көз карандысыз жана көз каранды өзгөрмөлөрүңүздү аныктаңыз. Ар бир өзгөрмөнүн үзгүлтүксүз же үзгүлтүксүз экендигин аныктоо менен графиктин туура түрүн тандаңыз. X жана Y огунда бара турган маанилерди аныктаңыз. X жана Y огуна, анын ичинде бирдиктерди белгилеңиз. Берилиштериңизди графикке салыңыз
Координаталык тегиздикте теңсиздиктин графигин кантип түзөсүз?
Үч кадам бар: Теңдемени "y" сол жакта, калганы оң жакта тургандай кылып кайра иретке келтириңиз. 'y=' сызыгын түзүңүз (аны y≤ же y≥ үчүн катуу сызык кылып, y үчүн сызык сызык кылыңыз) "чоң" (y> же y≥) үчүн сызыктын үстүнө көлөкө түшүрүңүз 'кичи' (y< же y≤)