Мазмуну:
Video: Координаталык тегиздикте теңсиздиктин графигин кантип түзөсүз?
2024 Автор: Miles Stephen | [email protected]. Акыркы өзгөртүү: 2023-12-15 23:38
Үч кадам бар:
- Теңдемени "y" сол жакта, калганы оң жакта тургандай кылып өзгөртүңүз.
- "y=" сызыгын түзүңүз (аны y≤ же y≥ үчүн катуу сызык, ал эми y үчүн сызыкча кылыңыз)
- "Көбүрөөк" (y> же y≥) үчүн сызыктын үстүнөн, же "кичинекейден" (y< же y≤) үчүн сызыктын астына көлөкө түшүрүңүз.
Ошо сыяктуу эле, координаталык тегиздикте графикти түзүүдө теңсиздикти көлөкөлөөнүн максаты эмне деп суралат?
Сен болгондо теңсиздиктердин графиктерин түзүү , болосуз график кадимки сызыктуу функциялар, биз мурункудай эле. Айырмачылыгы - бул маселени чечүү теңсиздик сызылган сызык эмес, нын аянты координаттык тегиздик бул канааттандырат теңсиздик.
Ошондой эле билесизби, теңсиздикти кантип табасыз? Бул нерселер теңсиздиктин багытына таасир этпейт:
- Санды эки тараптан тең кошуу (же кемитүү).
- Эки тарапты тең оң санга көбөйтүү (же бөлүү).
- Бир тарапты жөнөкөйлөтүү.
Ошо сыяктуу эле, сан сызыгында теңсиздиктин графигин кантип түзөсүз?
Жөн гана бул кадамдарды аткарыңыз
- Өзгөрмөнүн теңсиздик белгисинин экинчи тарабындагы санды табыңыз (х > 4теги 4 сыяктуу).
- Сан сызыгын чийиңиз жана ошол сандын айланасына ачык тегерек чийиңиз.
- Эгерде өзгөрмө ошол санга барабар болсо гана айлананы толтуруңуз.
- Өзгөрмө болушу мүмкүн болгон бардык сандарды көлөкө.
Теңдеменин чечиминин аныктамасы кандай?
А чечим ичинде теңдикти түзгөн белгисиз өзгөрмөлөргө туюнтмалардын дайындалышы теңдеме чын. Башкача айтканда, А чечим бул туюнтма же туюнтмалардын жыйындысы (ар бир белгисиз үчүн бирден), белгисиздердин ордуна коюлганда, теңдеме иденттүүлүккө айланат.
Сунушталууда:
Гиперболалык функциянын графигин кантип түзөсүз?
Гиперболалык функциялардын графиктери sinh(x) = (e x - e -x)/2. cosh(x) = (e x + e -x)/2. tanh(x) = sinh(x) / cosh(x) = (ex - e -x) / (ex + e -x) coth(x) = cosh(x) / sinh(x) = (ex + e - x) / (ex - e -x) sech(x) = 1 / cosh(x) = 2 / (ex + e -x) csch(x) = 1 / sinh(x) = 2 / (ex - e - x)
Координаталык тегиздикте кеңейүүнүн масштабдык факторун кантип табасыз?
A(2, 6), B(2, 2), C(6, 2) координаталары бар ABC үч бурчтугунун графигин түзүңүз. Андан кийин оригинал кеңейүү борбору катары сүрөттү масштабдуу 1/2 коэффициентине кеңейтиңиз. Биринчиден, координаталык тегиздикте баштапкы үч бурчтуктун графигин түзөбүз. Андан кийин, биз ар бир координатты 1/2 масштабдык факторуна көбөйтөбүз
Ылдамдыктын жана ылдамдануунун графигин кантип түзөсүз?
Принцип ылдамдык-убакыт графигиндеги сызыктын жантайышы объекттин ылдамдануусу жөнүндө пайдалуу маалыматты ачып берет. ылдамдануу нөл болсо, анда жантаюу нөл (б.а., горизонталдуу сызык). Эгерде ылдамдануу оң болсо, анда жантаюу оң болот (б.а., өйдө карай жантайыңкы сызык)
Геометрияда координаталык тегиздикти кантип түзөсүз?
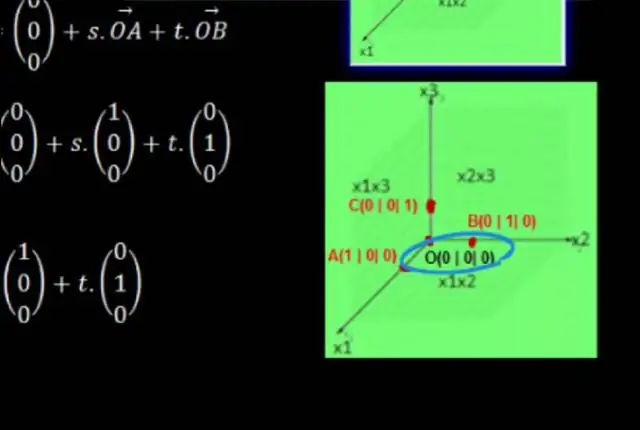
Координаталык тегиздикти түзүү үчүн төмөнкү кадамдарды аткарабыз: Эки сызыктын тең 0 чекитинде кесилишкен, бири-бирине перпендикуляр эки сан сызыгын тарткыла. Горизонталдык сан сызыгын x огу катары белгилеңиз жана вертикалдуу сан сызыгын у огу катары белгилеңиз
Бүтүн сандар жана рационал сандар деген эмне? Координаталык тегиздикте чекиттердин графиктери кантип түзүлөт?
Жогоруда айтылгандай, координаталык тегиздиктеги чекиттер (a, b) түрүндө көрсөтүлөт, мында a жана b рационал сандар. Рационал сандар – бөлчөк түрүндө жазыла турган сандар, p/q, мында p жана q бүтүн сандар. А чекиттин х координатасын, ал эми б чекиттин у координатын атайбыз