Мазмуну:
Video: Координаталык геометрияда батпакты кантип далилдейсиз?
2024 Автор: Miles Stephen | [email protected]. Акыркы өзгөртүү: 2023-12-15 23:38
Бул жерде эки ыкма бар:
- Эгерде төрт бурчтуктун ырааттуу эки жуп капталдары туура келсе, анда ал батперек (жылдын арткы бети батперек аныктамасы).
- Эгерде төрт бурчтуктун диагоналдарынын бири экинчисинин перпендикуляр биссектрисасы болсо, анда ал батперек (мүлктүн сөзү).
Кийинчерээк, кимдир бирөө батперек кандай өзгөчөлүктөргө ээ?
Батперек касиеттерге (1) эки жуп ырааттуу, конгруенттик тараптар, (2) конгруенттүү чоку эмес бурчтар жана (3) перпендикуляр диагоналдар кирет. Башка маанилүү көп бурчтук касиеттери трапециянын касиеттери, параллелограммдык касиеттери, ромб касиеттери, тик бурчтук жана квадраттык касиеттери менен тааныш болушу керек.
Ошондой эле билиңиз, тик бурчтук перпендикулярбы? Сол жактагы сүрөттөрдөн көрүнүп тургандай, а-нын диагоналдары тик бурчтук туура бурчта кесилишпейт (алар эмес перпендикуляр ). (Эгерде тик бурчтук квадрат болуп саналат.) Ал эми кесилишинен пайда болгон бурчтар дайыма эле бирдей өлчөм (өлчөм) боло бербейт. Карама-каршы борбордук бурчтар бирдей өлчөмдө (алар конгруенттүү.)
Андан кийин суроо туулат, батперек перпендикулярбы?
АНЫКТОО: А батперек бул төрт бурчтук, анын төрт тарабы чектеш эки башка жыйындысы бар сызылган, шайкеш тараптар. ТЕОРЕМА: Эгерде төрт бурчтуу батперек болуп саналат , диагоналдары болуп саналат перпендикуляр . ТЕОРЕМА: Эгерде төрт бурчтуу батперек болуп саналат , анын карама-каршы бир жуп бурчтары бар шайкеш.
Төрт бурчтук параллелограмбы?
А тик бурчтук карама-каршы эки жуп параллелдүү жана төрт тик бурчтары бар. Ал ошондой эле а параллелограмм , анткени анын эки жуп параллелдүү капталдары бар.
Сунушталууда:
Координаталык тегиздикте кеңейүүнүн масштабдык факторун кантип табасыз?
A(2, 6), B(2, 2), C(6, 2) координаталары бар ABC үч бурчтугунун графигин түзүңүз. Андан кийин оригинал кеңейүү борбору катары сүрөттү масштабдуу 1/2 коэффициентине кеңейтиңиз. Биринчиден, координаталык тегиздикте баштапкы үч бурчтуктун графигин түзөбүз. Андан кийин, биз ар бир координатты 1/2 масштабдык факторуна көбөйтөбүз
Координаталык тегиздикте теңсиздиктин графигин кантип түзөсүз?
Үч кадам бар: Теңдемени "y" сол жакта, калганы оң жакта тургандай кылып кайра иретке келтириңиз. 'y=' сызыгын түзүңүз (аны y≤ же y≥ үчүн катуу сызык кылып, y үчүн сызык сызык кылыңыз) "чоң" (y> же y≥) үчүн сызыктын үстүнө көлөкө түшүрүңүз 'кичи' (y< же y≤)
Геометрияда координаталык тегиздикти кантип түзөсүз?
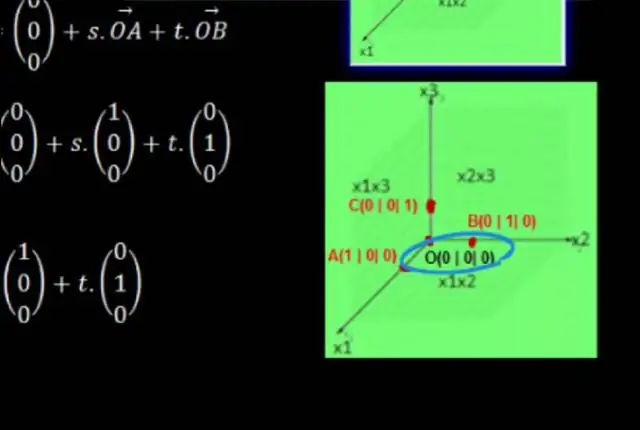
Координаталык тегиздикти түзүү үчүн төмөнкү кадамдарды аткарабыз: Эки сызыктын тең 0 чекитинде кесилишкен, бири-бирине перпендикуляр эки сан сызыгын тарткыла. Горизонталдык сан сызыгын x огу катары белгилеңиз жана вертикалдуу сан сызыгын у огу катары белгилеңиз
Координаталык тегиздик сизге тиешелүү тараптардын конгруенттүү экенин аныктоого кантип жардам берет?
Координаталык тегиздиктеги эки үч бурчтук берилгендиктен, алардын капталдарынын узундугун табуу үчүн аралык формуласын колдонуу менен алардын конгруенттүү экенин текшере аласыз. Эгерде үч жуп тарап бирдей болсо, анда үч бурчтуктар жогорудагы теорема боюнча конгруенттүү болот
Бүтүн сандар жана рационал сандар деген эмне? Координаталык тегиздикте чекиттердин графиктери кантип түзүлөт?
Жогоруда айтылгандай, координаталык тегиздиктеги чекиттер (a, b) түрүндө көрсөтүлөт, мында a жана b рационал сандар. Рационал сандар – бөлчөк түрүндө жазыла турган сандар, p/q, мында p жана q бүтүн сандар. А чекиттин х координатасын, ал эми б чекиттин у координатын атайбыз