Мазмуну:
Video: Абсолюттук маанилик теңсиздикти кантип жазуу керек?
2024 Автор: Miles Stephen | [email protected]. Акыркы өзгөртүү: 2023-12-15 23:38
Анын x = a жана x = -a эки чечими бар, анткени эки сан тең 0дөн a аралыкта. Сиз аны эки өзүнчө теңдеме кылып, анан аларды өзүнчө чечүүдөн баштайсыз. Ан абсолюттук маани теңдеменин чечими жок болсо абсолюттук маани туюнтма терс санга барабар, андыктан абсолюттук маани эч качан терс боло албайт.
Ошо сыяктуу эле, адамдар абсолюттук баалуулук үчүн кандай эрежелер бар?
Биз алып жатканда абсолюттук маани сандан, биз ар дайым оң сан (же нөл) менен аяктайт. Киргизүү оң же терс (же нөл) болгонуна карабастан, чыгаруу дайыма оң (же нөл) болот. Мисалы, | 3 | = 3, жана | –3 | = 3 да.
Ошондой эле, абсолюттук маанидеги теңсиздик бардык реалдуу сандар экенин кантип билесиз? The абсолюттук маани нын каалаган сан нөл (0) же оң. Бул мааниси бар ошол ал дайыма жогору болушу керек каалаган терс саны . Бул иштин жообу ар дайым бардык реалдуу сандар.
Ошондой эле билүү үчүн, сиз теңсиздиктин графигин кантип түзөсүз?
Сызыктуу теңсиздиктин графигин кантип түзүүгө болот
- Теңдемени "y" сол жакта, калганы оң жакта тургандай кылып өзгөртүңүз.
- "y=" сызыгын түзүңүз (аны y≤ же y≥ үчүн катуу сызык, y үчүн сызык сызык кылыңыз)
- "Көбүрөөк" (y> же y≥) үчүн сызыктын үстүнөн, же "кичинекейден" (y< же y≤) үчүн сызыктын астына көлөкө түшүрүңүз.
Татаал теңсиздиктин мисалы кандай?
жөнүндө ойлонуп көр мисал ныкы татаал теңсиздик : x < 5 жана x ≧ −1. Ар бир адамдын графиги теңсиздик түстө көрсөтүлөт. Сөздөн бери жана экөө кошулат теңсиздиктер , чечим эки чечимдин кайталанышы болуп саналат. Бул жерде бул эки сөз тең бир эле учурда чындык.
Сунушталууда:
Абсолюттук маанилик теңдеменин чечими жок экенин кантип билесиз?
Сандын абсолюттук мааниси анын нөлдөн алыстыгы. Бул сан ар дайым оң болот, анткени сиз бир нерседен эки фут алыстыкта терс боло албайсыз. Демек, терс санга барабар коюлган ар кандай абсолюттук чоңдук теңдеме, бул сан кандай экендигине карабастан, эч кандай чечим болуп саналбайт
13/4 аралаш сан катары кантип жазуу керек?
Терс туура эмес бөлчөк катары (|сан | > |бөлүүчү|): - 13/4 = - 13/4 Аралаш сан катары. (бир эле белгидеги бүтүн сан жана туура бөлчөк): - 13/4 = - 3 1/4 Процент менен: - 13/4 = - 325%
Y MX B стандарттуу түрдө кантип жазуу керек?
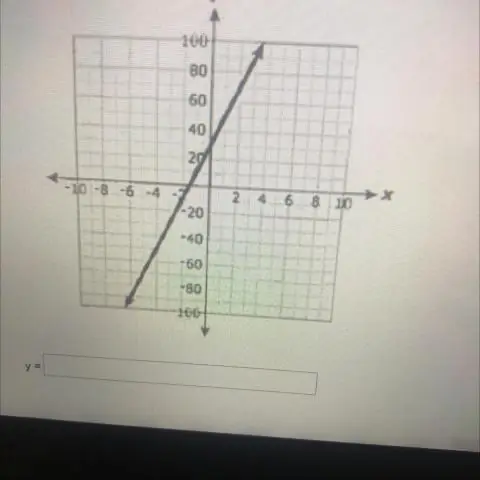
Мындай теңдеменин стандарттык түрү Ax + By + C = 0 же Ax + By = C. Бул теңдемени сол жагына y өз алдынча алуу үчүн кайра уюштурганда, ал у = mx +b түрүн алат. Бул жантайыңкы кесилиш формасы деп аталат, анткени m сызыктын эңкейишине барабар, ал эми b - у-нун x = 0 учурундагы мааниси, бул аны у-кесилиш кылат
Бөлчөктү бүтүн сан менен бирдик бөлчөктүн көбөйтүндүсү катары кантип жазуу керек?
Бирдик бөлчөк менен бүтүн сандын көбөйтүндүсүн табуу эрежелери Адегенде бүтүн санды бөлчөк деп жазабыз, б.а., аны бирге бөлүп жазабыз; мисалы: 7 71 деп жазылат. Андан кийин сандарды көбөйтөбүз. Биз бөлүүчүлөрдү көбөйтөбүз. Эгерде кандайдыр бир жөнөкөйлөштүрүү талап кылынса, анда ал аткарылат, андан кийин биз акыркы бөлчөктү жазабыз
Абсолюттук маанилик теңсиздиктин чечими жок экенин кантип билесиз?
Макул, эгерде абсолюттук маанилер ар дайым оң же нөл болсо, алар терс сандан аз же барабар болушу мүмкүн эмес. Демек, булардын эч биринин чечими жок. Бул учурда абсолюттук маани оң же нөл болсо, анда ал ар дайым терс сандан чоң же барабар болот