
Мазмуну:
- Автор Miles Stephen stephen@answers-science.com.
- Public 2024-01-18 08:17.
- Акыркы өзгөртүү 2025-06-01 05:05.
Чексиз топтомдун мисалдары:
- коюу тегиздиктин бардык чекиттеринин бир чексиз топтому .
- коюу сызык сегментиндеги бардык чекиттердин бири болуп саналат чексиз топтому .
- коюу 3кө эселенген оң бүтүн сандардын ичинен ан чексиз топтому .
- W = {0, 1, 2, 3, ……..} б.а. коюу бардык бүтүн сандардын бир чексиз топтому .
- N = {1, 2, 3, ……….}
- Z = {………
Ошо сыяктуу эле, сиз чексиз көптүктү кантип көрсөтө аласыз?
Сиз эки нерсени көрсөтүү менен көптүктү чексиз экенин далилдей аласыз:
- Берилген n үчүн анын узундугу n болгон жок дегенде бир элементи бар.
- Эгерде ал максималдуу чектүү узундуктагы элементке ээ болсо, анда сиз узунураак элементти кура аласыз (ушуну менен бул максималдуу чектүү узундуктагы элементти жокко чыгарат).
Экинчиден, топтомдун чексиз же чектүү экенин кантип айтасыз? Көптүктү чектүү же чексиз деп аныктоо үчүн пункттар:
- Эгерде топтомдун башталгыч жана аяктоочу чекитинин экөө тең болсо, анда ал чектүү, ал эми башталгыч же аяктоо чекити жок болсо, анда ал чексиз көптүк болуп саналат.
- Эгерде жыйында элементтердин саны чектелүү болсо, анда ал чектүү, ал эми анын элементтеринин саны чексиз болсо, анда ал чексиз.
Экинчиден, мисал менен чектүү жана чексиз деген эмне?
Мисалдар нын Infinite Sets Эгер коюу а эмес чектүү топтом , анда ал бир чексиз топтому . Натурал сандар жана бүтүн сандар эки мисалдар нын топтомдору ошол чексиз жана, демек, жок чектүү . Калың шрифттин баш тамгасы Z көп учурда белгилөө үчүн колдонулат коюу бүтүн сандардын.
Чексиз топтомдор барбы?
жок чексиз топтомдор . гана эмес чексиз топтомдорду жаса жок бар , бирок абдан түшүнүк логикалык карама-каршы - "чарчы тегерекчелерден" эч кандай айырмасы жок. Чексиз топтомдор математиканын заманбап негиздеринде түзмө-түз камтылган - «Аксиома Infinity ”.
Сунушталууда:
13/4 аралаш сан катары кантип жазуу керек?

Терс туура эмес бөлчөк катары (|сан | > |бөлүүчү|): - 13/4 = - 13/4 Аралаш сан катары. (бир эле белгидеги бүтүн сан жана туура бөлчөк): - 13/4 = - 3 1/4 Процент менен: - 13/4 = - 325%
Y MX B стандарттуу түрдө кантип жазуу керек?
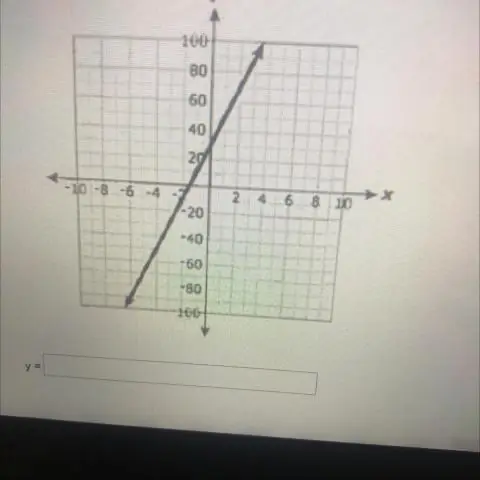
Мындай теңдеменин стандарттык түрү Ax + By + C = 0 же Ax + By = C. Бул теңдемени сол жагына y өз алдынча алуу үчүн кайра уюштурганда, ал у = mx +b түрүн алат. Бул жантайыңкы кесилиш формасы деп аталат, анткени m сызыктын эңкейишине барабар, ал эми b - у-нун x = 0 учурундагы мааниси, бул аны у-кесилиш кылат
Бөлчөктү бүтүн сан менен бирдик бөлчөктүн көбөйтүндүсү катары кантип жазуу керек?

Бирдик бөлчөк менен бүтүн сандын көбөйтүндүсүн табуу эрежелери Адегенде бүтүн санды бөлчөк деп жазабыз, б.а., аны бирге бөлүп жазабыз; мисалы: 7 71 деп жазылат. Андан кийин сандарды көбөйтөбүз. Биз бөлүүчүлөрдү көбөйтөбүз. Эгерде кандайдыр бир жөнөкөйлөштүрүү талап кылынса, анда ал аткарылат, андан кийин биз акыркы бөлчөктү жазабыз
Он белгинин күчү менен санды кантип жазуу керек?

Он белгинин даражасында чоң сандар он даражага же көрсөткүчкө карата жазылат. Көрсөткүч сиз жазгыңыз келген санга барабар болуу үчүн онду канча эсе эселфке көбөйтүү керектигин айтат. Мисалы, 100 10x10 = 102 деп жазылышы мүмкүн. 10 000 = 10x10x10x10 = 104
Пуннетт квадратын кантип жазуу керек?

Төрт бөлүккө бөлүнгөн квадратты тартыңыз. Ар бир ата-эненин генотибин чоң квадраттын жогору жагындагы ар бир кичинекей кутучанын үстүнө, ал эми калган ата-энелердин генотиптерин ар бир кичинекей кутучанын жанына сол жагына (өйдө ылдыйга) коюңуз. Рецессивдүү аллель же кичине тамга чоң тамгадан кийин келет
