Video: Эки популяцияны салыштырганда Стандарттык четтөө канчалык чоң болсо, дисперсия ошончолук көп?
2024 Автор: Miles Stephen | [email protected]. Акыркы өзгөртүү: 2023-12-15 23:38
Эки популяцияны салыштырганда стандарттык четтөө канчалык чоң болсо, дисперсия ошончолук көп бөлүштүрүү бар, эгерде кызыкчылыктын өзгөрмөсүнө караганда эки калк бирдей өлчөмгө ээ.
Ошентип, стандарттык четтөө эмне менен бирге колдонулат?
The стандарттык четтөө болуп саналат менен бирге колдонулат MEAN коңгуроо түрүндөгү бөлүштүрүүнү сандык түрдө сүрөттөйт. MEAN борборун өлчөйт? бөлүштүрүү, ал эми стандарттык четтөө бөлүштүрүүнүн таралышын өлчөйт.
Андан тышкары, статистикада эмпирикалык эреже деген эмне? The эмпирикалык эреже нормалдуу бөлүштүрүү үчүн, дээрлик бардык маалыматтар орточо үч стандарттык четтөөлөр чегинде болот деп айтылат. The эмпирикалык эреже үч бөлүккө бөлүүгө болот: маалыматтардын 68% ортодон биринчи стандарттык четтөөнүн чегинде болот. 95% эки стандарттык четтөөлөргө туура келет.
Ушуга байланыштуу, дисперсиялык өлчөм катары диапазонун чектөөсү кандай?
RANGE . The диапазон маалыматтардагы эң чоң жана эң кичине байкоонун ортосундагы айырма. Мунун биринчи артыкчылыгы дисперсиялык өлчөм аны эсептөө үчүн жеңил болуп саналат. Башка жагынан алганда, анын көптөгөн кемчиликтери бар.
Байкоо орточо көрсөткүчтөн стандарттык четтөөлөрдүн санын кандай көрсөтөт?
Z-упайы көбүнчө стандартташтырылган маани деп аталат. Z-упайлары өлчөө стандарттык четтөөлөрдүн саны жогору же ылдый болуп саналат дегенди билдирет . Мис. z-score1.24 "маалыматтын мааниси 1.24" деп чечмеленет стандарттык четтөө үстүндө дегенди билдирет ."
Сунушталууда:
Стандарттык четтөө эмне менен бирге колдонулат?
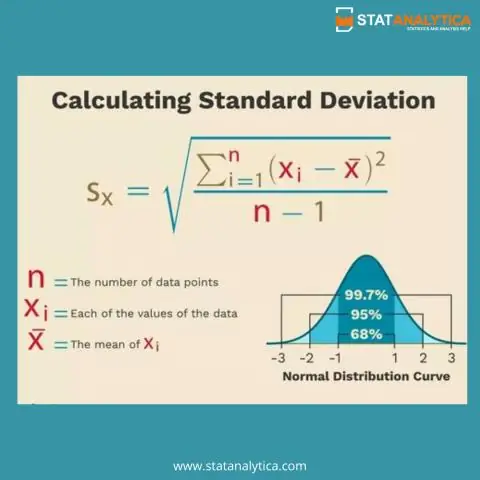
Стандарттык четтөө коңгуроо түрүндөгү бөлүштүрүүнү сандык түрдө сүрөттөө үчүн MEAN менен бирге колдонулат. MEAN борборун өлчөйт? бөлүштүрүү, ал эми стандарттык четтөө бөлүштүрүүнүн ТАРАЛУУну өлчөйт
Таблицадагы стандарттык четтөө деген эмне?
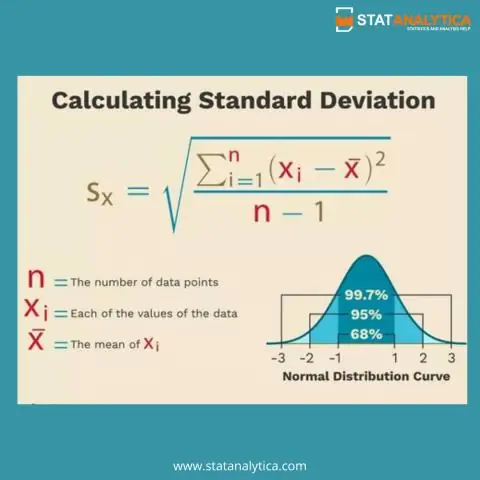
Стандарттык четтөө - бул маалыматтардын орточодон канчалык таралышынын өлчөмү. Таблицада стандарттык четтөөнү табуу жөн гана өлчөөнүн агрегациясын өзгөртүүнү камтыйт. Калктын жана үлгүдөгү стандарттык четтөөлөрдүн экөө тең камтылган топтоо варианттары
Эң чоң тешик канчалык чоң?
650 футтан ашык тереңдикте, Диндин Көк Тешиги дүйнөдөгү эң терең чуңкур болуп саналат, анын кире бериши суунун астында. Багам аралындагы Лонг-Айленддеги Кларенс Таун шаарынын батышындагы булуңда жайгашкан, анын көрүнгөн диаметри болжол менен 82–115 фут
Стандарттык четтөө тести деген эмне?
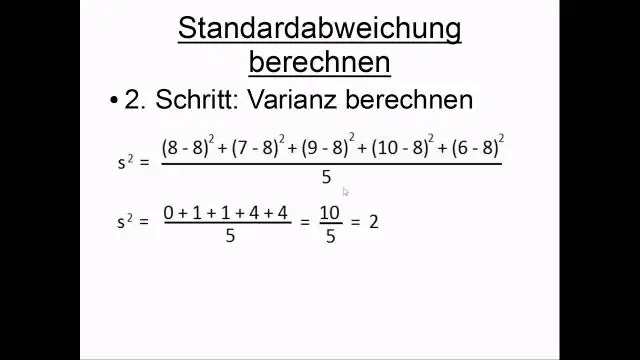
Стандарттык четтөө, ошондой эле түпкү орточо квадраттык четтөө деп аталат, упайлар орточодон четтеген орточо аралык үчүн өзгөрмөлүүлүктүн өлчөмү болуп саналат. Ал дисперсиянын квадрат тамырын алуу менен эсептелет. Стандарттык четтөө дайыма оң: SD>0. Стандарттык четтөө өзгөрмөлүүлүктүн өлчөмү болуп саналат
Жазуунун үлгүсүн шектүү документке салыштырганда документтердин ортосундагы жаш айырмачылык он эки айдан ашпоого тийиш?
Шектүү жазуу үлгүсүн салыштырганда? документ, документтердин ортосундагы жаш айырмасы алты айдан он эки айдан ашпоого тийиш. Салыштыруунун жыйынтыгын аныктоо үчүн үлгүлөрдүн жетиштүү саны абдан маанилүү